Theoreom:
(Van Khea):Let  . Prove that:
. Prove that:
Let  and
and  such that
such that  . We get:
. We get:
Let 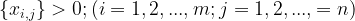 and for
and for  such that:
such that: 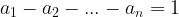 . So we get:
. So we get:
Theoreom:
(Van Khea) :Let be positive real numbers and let
. For all
be real numbers satisfying
and
. So we have:
Equality hold when:
Theoreom:
(Van Khea): For a real convex fruction numbers
in its domain
, and positive
so we can write that:
For a real concave fruction  numbers
numbers  in its domain
in its domain  , and positive
, and positive  so we can write that:
so we can write that:
Theoreom:
(Van Khea): Let be positive real numbers and satisfying
. So we have:
Theoreom:
(Van Khea): Let . So we have
Theoreom:
(Van Khea): Let be positive real numbers and for all
satisfy
. So we have:
និង
Theorem:
(Van Khea) :1/ Let a real convex function for all
in its domain. Suppose that for all positive real numbers
satisfies
in its domain and
. Then we have:
.
2/ Let a real concave function for all
in its domain. Suppose that for all positive real numbers
satisfies
in its domain and
. Then we have:
.
Theorem:
(Van Khea): Let  is a convex function. For any positive real numbers
is a convex function. For any positive real numbers 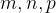 that
that 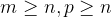 and
and  . So for
. So for  we can stat as:
we can stat as:
Special case:
- If
- If
then
Theorem:
(van khea): 1/ Let be positive real numbers such that
. So we have:
(van khea):2/ Let be positive real numbers such that
. So we have:
Theoreom:
(van khea): Let be positive real numbers such that:
or
.Then
Theoreom:
(van khea): Let be positive real numbers such that:
or
.Then
Theoreom:
(van khea): Consider where
and
or
. Let
be convex function or momotonic and let
where
in the same neture. Then:
Theoreom:
(van khea): Consider where
and
or
. Let
be convex function or momotonic and let
where
in the same neture. Then:
Theorem:
(van khea): Let then we have:










Leave a comment