August 10, 2010
August 1, 2010
Problem 045 (Van Khea)
Let  be positive real numbers and satisfying
be positive real numbers and satisfying  . Prove that if
. Prove that if  and
and 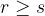 then we have
then we have
Proof
We have 
Let 
Let 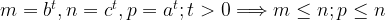
From the inequality by Van Khea for  and
and  we have
we have
Example1: Let  then we have
then we have 
Example2: Let  then we have
then we have
See also the inequality by Van Khea
Problem 044
Let  be positive real numbers and satisfying
be positive real numbers and satisfying  . Prove that:
. Prove that:
-
If
then we have
-
If
then we have
Proof
We have 
Let 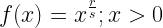
-
If
then
So from the inequality by VanKhea for
 and
and  we get
we get
-
If
then we have
So from the inequality by Van Khea for
and
we get:
Van Khea
See also the inequality by van khea
Problem 041
Let 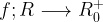 and
and 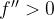 . For
. For  be positive real numbers and satisfying
be positive real numbers and satisfying  . Prove that:
. Prove that:
Van Khea
Problem 040
Let  and
and 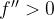 . For
. For  be positive real numbers and satisfying
be positive real numbers and satisfying  . Prove that:
. Prove that:
Van Khea
Problem 039
Let  and
and 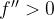 . For
. For  be positive real numbers and satisfying
be positive real numbers and satisfying 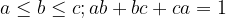 ; Prove that:
; Prove that:
Proof
From the problem 038 we have
From Jensen’s inequality for  we have
we have
Therefore the proof is completed.
Van Khea
Problem 038
Let  and
and 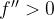 . For all
. For all  ; Prove that:
; Prove that:
Proof
Let  but we have
but we have 
From the inequality by van khea for  and
and 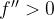 we have
we have
Therefor the proof is completed.
Van Khea









